NP-Completeness | Tractable and Intractable Problems | Polynomial time reduction | DAA

 NP-Completeness

Most of the problems considered up to now can be solved by algorithms in worst-case polynomial time. There are many problems and it is not necessary that all the problems have an apparent solution. This concept, somehow, can be applied to solving the problem using computers. The computer can solve: some problems in a limited time e.g. sorting, some problems require an unmanageable amount of time e.g. Hamiltonian cycles, and some problems cannot be solved e.g. I-lasting Problem. In this section, we concentrate on the specific class of problems called NP-complete problems (will be defined later).

Tractable and Intractable Problems

We call problems as tractable or easy if the problem can be solved using polynomial-time algorithms. The problems that cannot be solved in polynomial time but require a super polynomial-time algorithm are called intractable or hard problems. There are many problems for which no algorithm with running time better than exponential time is known some of them are, the traveling salesman problem, Hamiltonian cycles, circuit satisfiability, etc.

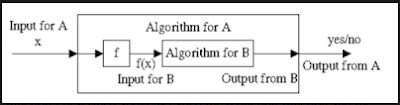
Polynomial-time reduction

Given two problems A and B, a polynomial-time reduction from A to B is a polynomial-time function f that transforms the instances of A into instances of B such that the output of the algorithm for the problem A on input instance x must be the same as the output of the algorithm for the problem B on input instance fix} as shown in the figure below. If there is polynomial-time computable function f such that it is possible to reduce A to B, then it is denoted as A <=p B. The function f described above is called the reduction function and the algorithm for computing f is called the reduction algorithm.

P and NP classes and NP-completeness

The set of problems that can be solved using the polynomial-time algorithm is regarded as class P. The problems that are verifiable in polynomial time constitute the class NP. The class of NP-complete problems consists of those problems that are NP as well as they are as hard as any problem in NP (more on this later). The main concern of studying NP-completeness is to understand how hard the problem is. So if we can find some problem as NP-complete then we try to solve the problem using methods like approximation, rather than searching for the faster algorithm for solving the problem exactly.

Complexity Class P

P is the class of problems that can be solved in polynomial time on a deterministic effective computing system (ECS). Loosely speaking, all computing machines that exist in the real world are deterministic ECSs. So P is the class of things that can be computed in polynomial time on real computers.

Complexity Class NP

NP is the class of problems that can be solved in polynomial time on a non—deterministic effective computing system (ECS) or we can say that “NP is the class of problems that can be solved in super polynomial time on a deterministic effective computing system {EC S)”. Loosely speaking, all computing machines that exist in the real world are deterministic ECSs. So NP is the class of problems that can be computed in super polynomial time on real computers. But problems of class NP are verifiable in polynomial time. Using the above idea we say the problem is in class NP (nondeterministic polynomial time} if there is an algorithm for the problem that
verifies the problem in polynomial time. For e.g. Circuit satisfiability problem (SAT) is the question “Given a Boolean combinational circuit, is it satisfiable? i.e. does the circuit has an assignment sequence of truth values that produces the output of the circuit as l?" Given the circuit satisfiability problem take a circuit x and a certificate y with the set of values that produce output 1, we can verify that whether the given certificate satisfies the circuit in polynomial time. So we can say that the circuit satisfiability problem is NP.

The complexity of Class NP-Complete

NP-complete problems are those problems that are the hardest problems in class NP. We define some problems say A, is NP-complete if
a. A ∈  NP, and
b. B <=p A, for every B ∈ NP. 
The problem satisfying property b is called NP-hard.
NP-Complete problems arise in many domains like boolean logic; graphs, sets, and partitions; sequencing, scheduling, allocation; automata and language theory; network design; compilers, program optimization; hardware design optimization; number theory, algebra, etc.