DOOLITTLE Algorithm
In the numerical method Doolittle Algorithm : LU Decomposition Algorithm (where LU stands for Lower and Upper and also called LU factorization Algorithm) factors a matrix as the product of a lower triangular matrix and an upper triangular matrix. Computers usually solve square systems of linear equations using the LU decomposition, and it is also a key step when inverting a matrix, or computing the determinant of a matrix.
Let A be a square matrix. An LU factorization algorithm refers to the factorization of A, with proper row and/or column orderings or permutations, into two factors, a lower triangular matrix L and an upper triangular matrix U, A=LU.
Assume that A has a Crout factorization A = LU.
It is always possible to factor a square matrix into a lower triangular matrix and an upper triangular matrix. That is, [A] = [L][U]
Doolittle’s method provides an alternative way to factor A into an LU decomposition without going through the hassle of Gaussian Elimination.
For a general n×n matrix A, we assume that an LU decomposition exists, and write the form of L and U explicitly. We then systematically solve for the entries in L and U from the equations that result from the multiplications necessary for A=LU.
#include<stdio.h>
#include<conio.h>
#include<math.h>
int main(){
int n,i,k,j;
float sum=0,a[10][10],u[10][10],l[10][10],b[10],x[10],z[10];
printf("Do-Little LU Decomposition");
printf("\nEnter Dimension of System of equation\n");
scanf("%d",&n);
printf("\nEnter the coefficients of the Matrix\n");
for(i=0;i<n; i++)
for(j=0;j<n;j++){
scanf("%f",&a[i][j]);
}
printf("Enter RHS vector\n");
for(i=0; i<n; i++){
scanf("%f",&b[i]);
}
//Compute Elements of L and U matrix
for(j=0; j<n; j++)
u[0][j]=a[0][j];
for(i=0;i<n;i++)
l[i][i]=1;
for(i=1; i<n; i++)
l[i][0]=a[i][0]/u[0][0];
for(j=1;j<n;j++){
for(i=1; i<=j;i++){
for(k=0;k<=i-1;k++){
sum=sum+(l[i][k]*u[k][j]);
}
u[i][j]=a[i][j]-sum;
sum=0;
}
for(i=j+1;i<n;i++){
for(k=0;k<=j-1;k++){
sum=sum+(l[i][k]*u[k][j]);
}
l[i][j]=(a[i][j]-sum)/u[j][j];
sum=0;
}
}
//Solve for Z using forward subsitution
z[0]=b[0];
for(i=1;i<n;i++){
for(j=0; j<i; j++)
sum=sum+(l[i][j]*z[j]);
z[i]=b[i]-sum;
sum=0;
}
// solve for X using Backward subsitution
x[n-1]= z[n-1]/u[n-1][n-1];
for(i=n-2;i>=0;i--){
for(j=i+1;j<n;j++)
sum=sum+(u[i][j]*x[j]);
x[i]=(z[i]-sum)/u[i][i];
sum=0;
}
printf("\nSolution:\n");
for(i=0; i<n;i++){
printf("x%d=%f\t",i+1,x[i]);
}
getch();
return 0;
}
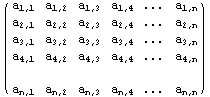
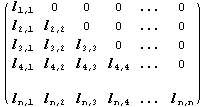




Comments
Post a Comment
Subscribe Us and Thanks for visiting blog.