Heap Sort

Heap Sort  

A heap is a nearly complete binary tree with the following two properties:

• Structural property: all levels are full, except possibly the last one, which is filled from left to right
• Order (heap) property: for any node x, Parent(x) ≥ x

Array Representation of Heaps

• A heap can be stored as an array A.
• Root of tree is A[1]
• Left child of A[i] = A[2i]
• Right child of A[i] = A[2i + 1]
• Parent of A[i] = A[ i/2 ]
• Heapsize[A] ≤ length[A]

The elements in the subarray A[(⌊n/2⌋+1) .. n] are leaves

Max-heaps (largest element at root), have the max-heap property:  

• for all nodes i, excluding the root:    

A[PARENT(i)] ≥ A[i]

Min-heaps (smallest element at root), have the min-heap property:

• for all nodes i, excluding the root:  

A[PARENT(i)] ≤ A[i]

Adding/Deleting Nodes

New nodes are always inserted at the bottom level (left to right) and nodes are removed from the bottom level (right to left).

Operations on Heaps

• Maintain/Restore the max-heap property
  
  1. MAX-HEAPIFY
• Create a max-heap from an unordered array
  
  1. BUILD-MAX-HEAP
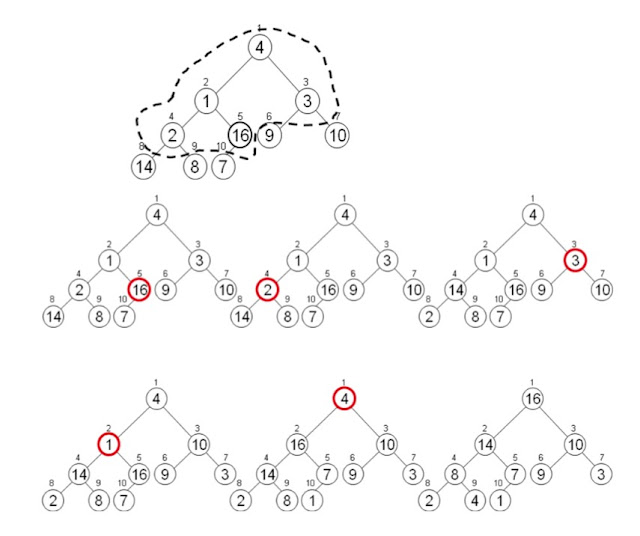
• Sort an array in place
  
  1. HEAPSORT
• Priority queues

Heapify Property

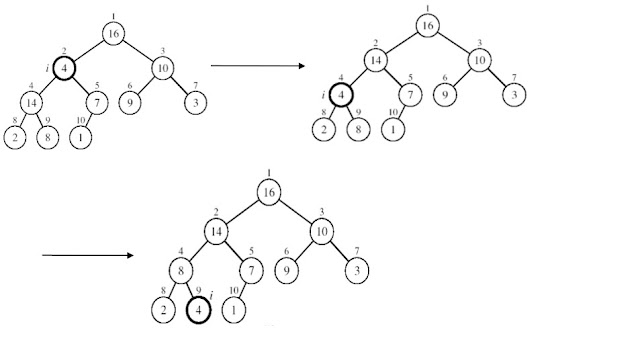
Suppose a node is smaller than a child and Left and Right subtrees of i are max-heaps. To eliminate the violation:  

• Exchange with larger child
• Move down the tree
• Continue until node is not smaller than children

Algorithm

Max - Heapify(A, i, n)
{
    l = Left(i)
        r = Right(i)
            largest = i;
    if l
        ≤ n and A[l] > A[largest]
            largest = l
                      if r ≤ n and
                      A[r] > A[largest]
                          largest = r
                                    if largest≠i
                                    exchange(A[i], A[largest])
                                        Max -
                                    Heapify(A, largest, n)
}

Analysis:  

In the worst case Max-Heapify is called recursively h times, where h is height of the heap and since each call to the heapify takes constant time

Time complexity = O(h) = O(logn)

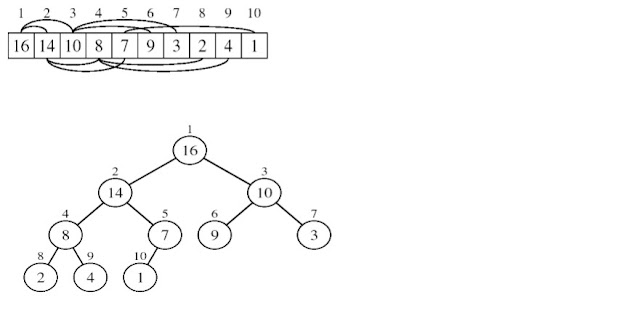
Building a Heap

Convert an array A[1 … n] into a max-heap (n = length[A]). The elements in the sub-array A[(⌊n/2⌋+1) .. n] are leaves. Apply MAX-HEAPIFY on elements between 1 and ⌊n/2⌋.

Algorithm:  

Build-Max-Heap(A)

n = length[A]  

for i ← ⌊n/2⌋ down to 1        

do MAX-HEAPIFY(A, i, n)

Time Complexity:

Running time:  Loop executes O(n) times and complexity of Heapify is O(lgn), therefore complexity of Build-Max-Heap is O(nlogn).

This is not an asymptotically tight upper bound