Laplace Algorithm
Laplace’s approximation is one of the most fundamental asymptotic techniques for the estimation of integrals containing a large parameter or variable. For integrals of the form
where f(t) and ψ(t) are real continuous functions defined on the interval [a,b](which may be infinite), the dominant contribution as x→+∞ arises from a neighborhood of the point where ψ(t) attains its maximum value. When ψ(t)possesses a single maximum at the point t0∈(a,b), so that ψ′(t0)=0, ψ″(t0)<0 span="">and f(t0)≠0, then I(x) has the asymptotic behavior
Abstract
A new algorithm for the numerical inversion of Laplace transforms is presented. The algorithm requires that transform values F(z) are available at arbitrary points in the complex z plane. It involves the approximation of the exponential function est in the inversion integral by a two-parameter function. The approximated inversion integral is then expanded into two different infinite series:
- partial fraction expansion by the Mittag-Leffler theorem;
- power series expansion in est.
In the numerical procedures, the summing of the infinite series are accelerated by a Wynn's type of in -algorithm. Trial runs on several test functions show that the results are highly accurate. The programming effort for the algorithm is minimal in comparison with other algorithms of comparable accuracy. The computation involves only a finite small number of function evaluations of the transform function. The method is believed to work for a wider range of functions since the algorithm does not make any assumption on representing f(t) by a linear combination of a certain class of basis functions.
C Code For Laplace Algorithm
#include<stdio.h>
#include<conio.h>
#include<math.h>
int main(){
int n,i,j,k;
float sum,error,E[10],a[10][10],b[10],new_x[10],old_x[10],tl,tr,tu,tb;
printf("\nLaplace \n");
printf("Enter the dimension of plate\n");
scanf("%d",&n);
printf("\nEnter the temperatures at left, right, bottom and top of the plate \n");
scanf("%f%f%f%f",&tl,&tr,&tb,&tu);
//construction of coefficient matrix
for(i=0;i<=n;i++)
a[i][i]=-4;
for(i=0;i<=n;i++)
a[i][n-i]=0;
for(i=0;i<=n;i++)
for(j=0;j<=n;j++){
if(i!=j && j!=(n-i))
a[i][j]=1;
}
//Construction of RHS vector
for(i=0;i<=n;i++)
b[i]=0;
k=0;
for(i=1;i<n;i++){
for(j=1;j<n;j++){
if((i-1)==0)
b[k]=b[k]-tl;
if((i+1)==n)
b[k]=b[k]-tr;
if((j-1)==0)
b[k]=b[k]-tb;
if((j+1)==n)
b[k]=b[k]-tu;
k++;
}
}
printf("\nEnter accuracy limit\n");
scanf("%f",&error);
//Solving the system of linear equations using Gauss-Seidel method
for(i=0;i<=n;i++){
new_x[i]=0;
}
while(1){
for(i=0;i<=n;i++){
sum=b[i];
for(j=0;j<=n;j++){
if(i!=j)
sum=sum-a[i][j]*new_x[j];
}
old_x[i]=new_x[i];
new_x[i]=sum/a[i][i];
E[i]=fabs(new_x[i]-old_x[i])/fabs(new_x[i]);
}
for(i=0;i<=n;i++){
if(E[i]>error)
break;
}
if(i==(n+1))
break;
else
continue;
}
printf("\nsolution\n");
for(i=0;i<=n;i++)
printf("x%d=%6.2f\n",i+1,new_x[i]);
getch();
return 0;
}
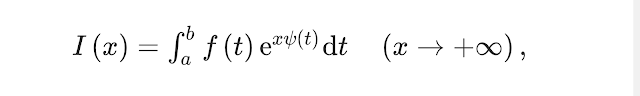



Comments
Post a Comment
Subscribe Us and Thanks for visiting blog.